Chapter 4: Integration
Up to this point, we have overlooked the other half of calculus—integral calculus. In Chapter 2 we learned to differentiate any function, but how do we go backward—that is, if we have \(f',\) then how do we get \(f \ques\) For example, if we have a particle's velocity function, then how do we get its position? Additionally, of what use is the area under a curve, and is it even possible to calculate it exactly? Yes! Just as we used limits in Section 2.1 to calculate the slope of a tangent line, in this chapter we apply limits again to determine the exact area bounded by a curve. Also in this chapter, we will learn a majestic theorem that links differential calculus to integral calculus. This theorem forms an inseparable bond between antidifferentiation (the inverse process of differentiation) and calculating the areas bounded by curves.
Sections
4.3 Fundamental Theorem of Calculus
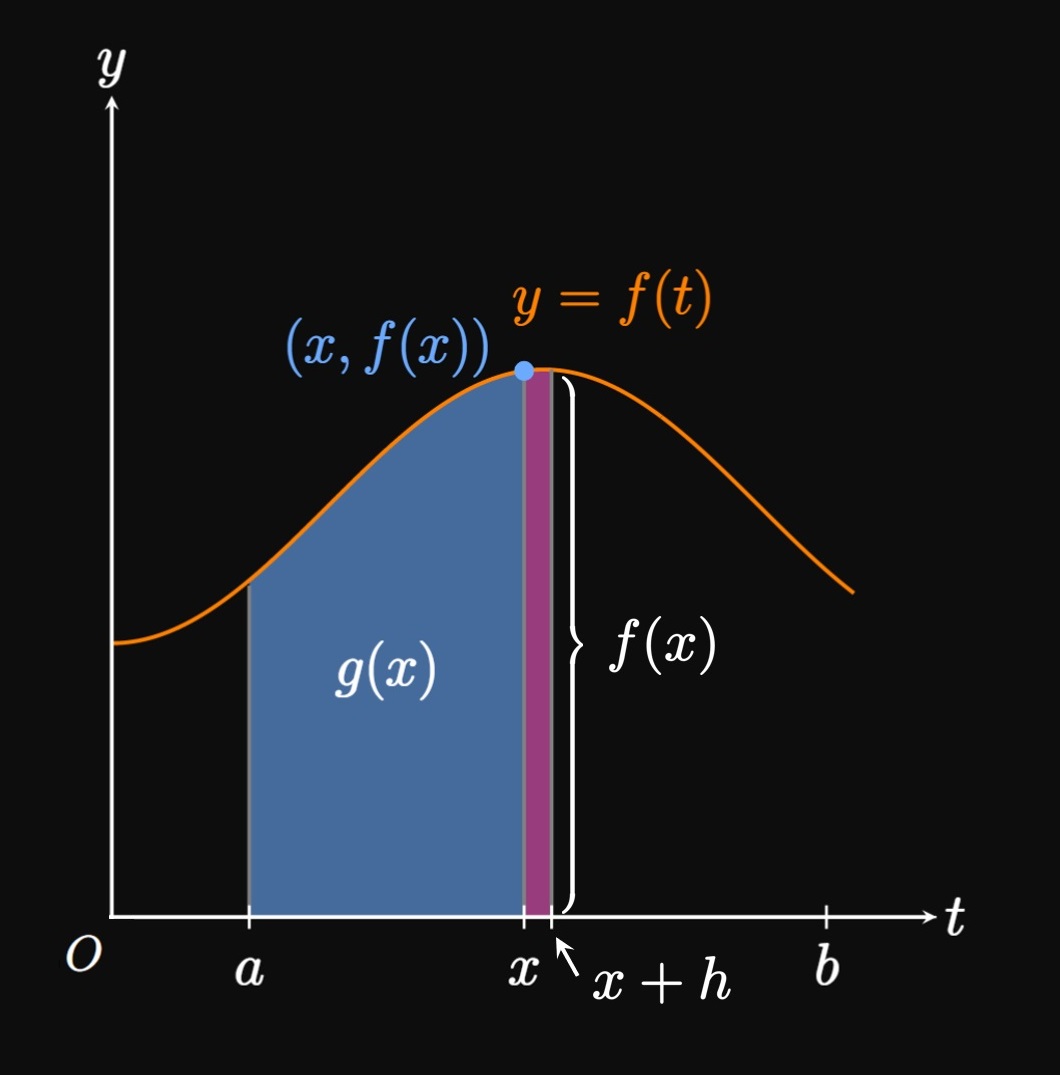
Fundamental Theorem of Calculus, Part I and Part II, to evaluate definite integrals. Discussion of Chain Rule in Part I. Proof and geometric intuition. Net Change Theorem. Transformation of an integral using a substitution. Discussion of changing of bounds and inclusion of Fundamental Theorem of Calculus. Antiderivatives of all six trigonometric functions. Integrals with odd and even functions by symmetry. Endpoint approximations, the Midpoint Rule, and the Trapezoidal Rule, with error bounds. Discussion of when each approach is an underestimate or overestimate. Derivation of Simpson's Rule, with error bound.