Chapter 5: Applications of Integration
In Chapter 4 we learned to calculate definite integrals. But what more can be done with integrals? In this chapter we will learn to calculate the areas bounded by multiple curves, the work done by a force, and the average value of a function. Integrals are also key to calculating the volumes of solids; we will begin by calculating solids of known cross sections, and then investigate the solids generated by rotating regions about axes—all through the process of accumulation.
Sections
Use of definite integrals to calculate areas of bounded regions. Integrating vertically and horizontally, given functions expressed in \(x\) or \(y.\)
5.2 Volumes with Cross Sections
Finding the volume of a solid whose base lies in a plane and whose cross-sections are geometric figures. Use of the Disk Method and Washer Method to calculate the volume of the solid generated when a bounded region is spun around an axis. Includes horizontal and vertical axes of rotation. Geometric intuition, figures, and animations.5.4 Shell Method
Using cylindrical shells to calculate the volume of a solid generated by rotating a region about a line. Integration with both \(x\) and \(y.\)5.5 Work
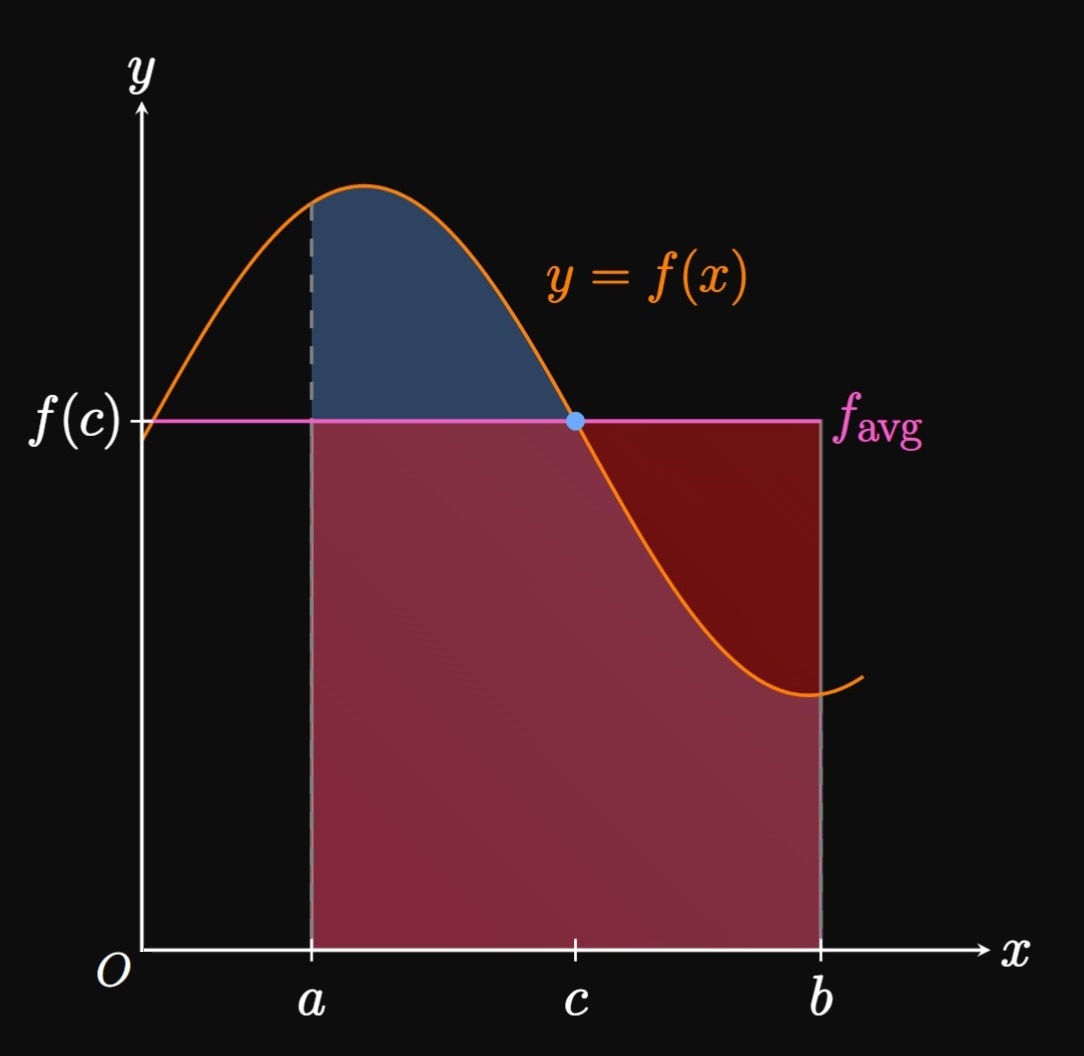
Work done by a force. Applications involving a variable force, springs, gases, lifting cables, and pumping water out of tanks. Average value of a function and Mean Value Theorem for Integrals, with proof.