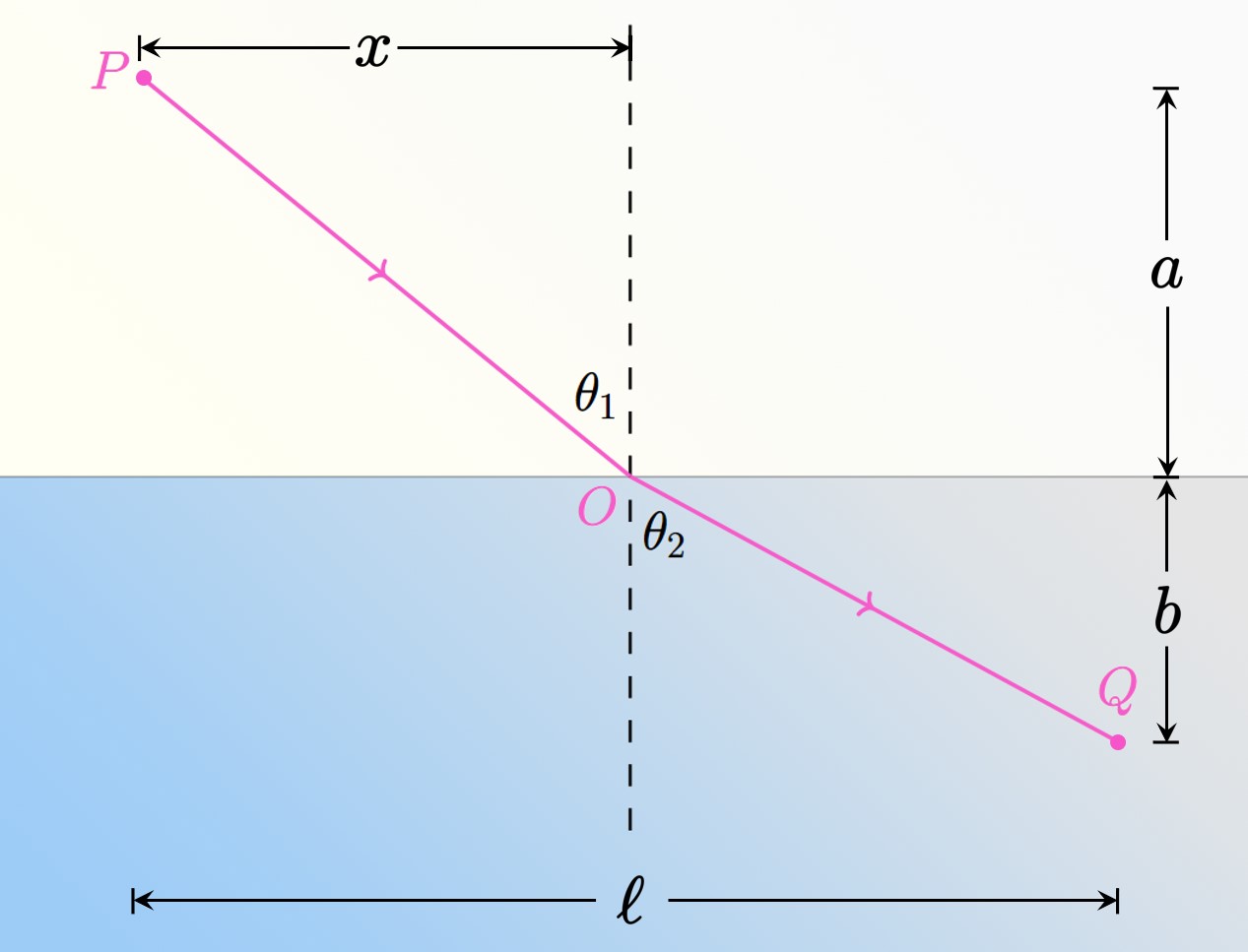
Chapter 3 Challenge Problems Solutions
Quadratic Fitting Substituting \(C(0) = 500\) shows \[ \ba C(0) = a(0)^2 + b(0) + c &= 500 \nl \implies c &= 500 \pd \ea \] Then substituting \(C(100) = 700\) yields \begin{align} C(100) = a(100)^2 + b(100) + 500 &= 700 \nonum \nl 10000a + 100b &= 200 \pd \label{eq:C-1} \end{align} Likewise, substituting \(C(200) = 950\) gives \begin{align} C(200) = a(200)^2 + b(200) + 500 &= 950 \nonum \nl 40000a + 200b &= 450 \pd \label{eq:C-2} \end{align} Multiplying \(\eqref{eq:C-1}\) by \(2\) and subtracting it from \(\eqref{eq:C-2},\) we get \[ \ba 40000a + 200b - 2(10000a + 100b) &= 450 - 2(200) \nl 20000a &= 50 \nl \implies a &= 0.0025 \pd \ea \] (See Section 0.5 to review solving systems of linear equations.) To solve for \(b,\) we substitute \(a = 0.0025\) back into either equation of the system—for example, into \(\eqref{eq:C-1} \col\) \[ \ba 10000(0.0025) + 100b &= 200 \nl \implies b &= 1.75 \pd \ea \] Hence, the identity of the cost function is \[C(x) = \boxed{0.0025x^2 + 1.75x + 500}\]
Predicted Cost The predicted cost of producing \(300\) units is \[C(300) = 0.0025(300)^2 + 1.75(300) + 500 = \boxed{\$1250}\]
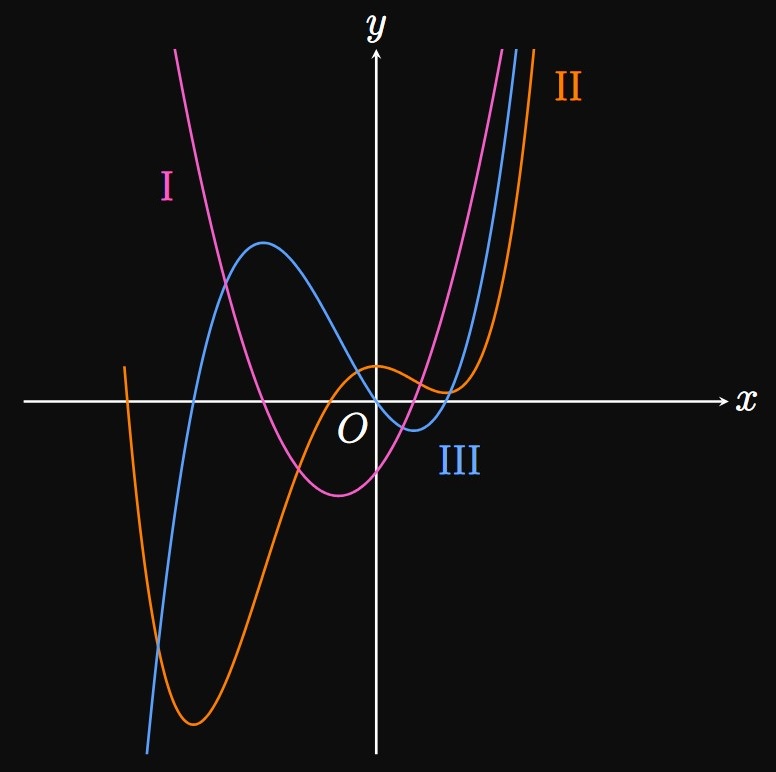
- \(p \gt 0\)
- \(p \lt 0\)
- If \(p > 0,\) then as \(x \to \infty,\) \[\ln x \to \infty \and x^p \to \infty \pd\] Therefore, \(\lim_{x \to \infty} k(x)\) is in the indeterminate form \(\indInfty.\) We then apply L'Hôpital's Rule to find \[ \ba \lim_{x \to \infty} \frac{\ln x}{x^p} &= \lim_{x \to \infty} \frac{1/x}{px^{p - 1}} \nl &= \lim_{x \to \infty} \frac{1}{px} \nl &= \boxed{0} \ea \]
- Let's introduce a new variable \(q\) such that \(q = -p.\) We then have \[\lim_{x \to \infty} k(x) = \lim_{x \to \infty} x^q \ln x \cmaa q \gt 0 \pd\] As \(x \to \infty,\) \(x^q\) and \(\ln x\) both approach \(\infty,\) so their product is also \(\infty.\) Therefore, \[\lim_{x \to \infty} k(x) = \infty\] (or alternatively, \(\lim_{x \to \infty} k(x)\) does not exist).
Verifying the Inequality Let \(f(x) = x\) and \(g(x) = \sin x.\) Then \(f(0) = g(0) = 0.\) Also, \(f'(x) = 1\) and \(g'(x)= \cos x.\) For \(0 \lt x \lt 2\pi,\) we have \(\cos x \lt 1\) and thus \(f'(x)\gt g'(x)\) on \((0,2\pi).\) Applying the preceding result on \([0,x]\) with \(x\in(0,2\pi)\) gives \[ f(x) \gt g(x) \implies x \gt \sin x \pd \] for all \(0 \lt x \lt 2 \pi.\)
The limit does not exist.Is Cady truly correct?